Words order, in a language, is very important because its alteration alters the sentence’s structure and hence its meaning. To integrate this piece of information into a model, we can use positional encoding. Positional encoding represent a word’s position in a sentence by a numerical vector. Positional encoding can be learned as it can be set or fixed.
Vaswani et al. propose to represent the position of a word by sine and cosine functions. This representation is unique and bounded (it won’t grow with the number of words).
The sine and cosine functions depend on the word’s position and the corresponding wavelength is different for each dimension of the desired encoded vectors. In particular, the positional encoding of a sequence of length $L$ is given by the matrix $\mathbf{V}$ of size $L\times D$ where $D$ is the dimension of the encoding. $\mathbf{V}$ is defined as,
$$\mathbf{V}_{l, 2d} = \sin\Bigg(\frac{l}{10000^\frac{2d}{D}}\Bigg), \quad \quad 0\leq l < L \text{ and } 0\leq d < \Big\lceil\frac{D}{2}\Big\rceil$$
$$\mathbf{V}_{l, 2d+1} = \cos\Bigg(\frac{l}{10000^\frac{2d}{D}}\Bigg) \quad \quad 0\leq l < L \text{ and } 0\leq d < \Big\lfloor\frac{D}{2}\Big\rfloor$$
Here Vaswani et al. consider waveforms with wavelengths that varies between $2\pi$ and $10000 \times 2\pi$
To understand how it works, we consider a scenario where the sequence length $L =100$ and the dimension of the encoding $D = 50$, and we plot the sine and cosine, as functions of $l$, for $d=0$, $d=1$, and $d=6$.

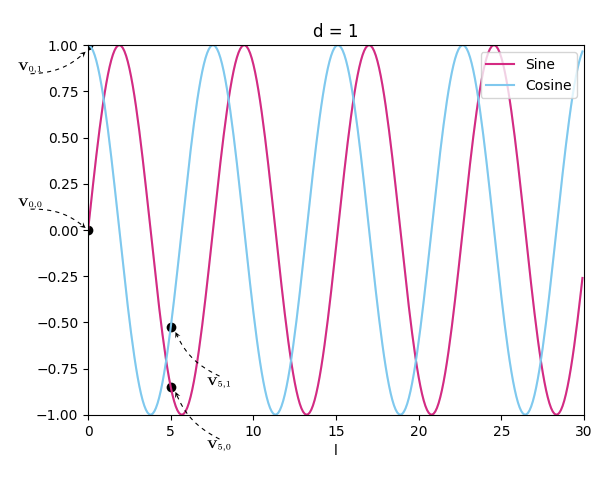
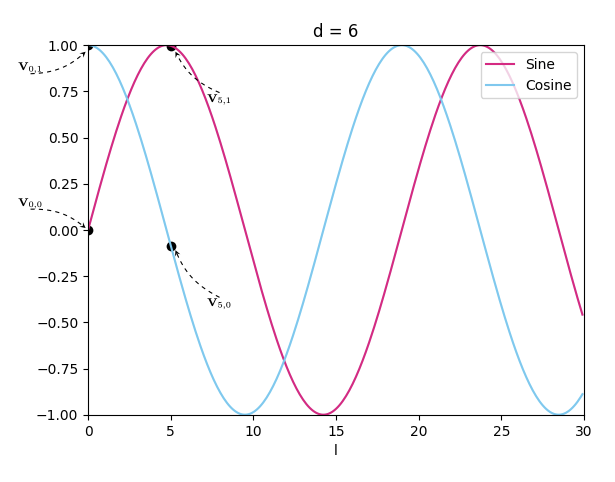
The positional encoding of the first word in the sequence is $\mathbf{V}_{0*} = \Big[\sin\big(0\big), \cos\big(0\big), \dots, \sin\big(0\big), \cos\big(0\big)\Big] = \Big[0, 1, \dots, 0, 1\Big]$. That was easy right?
Let’s consider the positional encoding of the fifth word in the sequence $\mathbf{V}_{5*} = \Bigg[\sin\big(5\big), \cos\big(5\big), \sin\Big(\frac{5}{10000^\frac{2}{50}}\Big), \cos\Big(\frac{5}{10000^\frac{2}{50}}\Big), \dots, \sin\Big(\frac{5}{10000}\Big), \cos\Big(\frac{5}{10000}\Big)\Bigg] = \Big[-0.96, 0.28, -0.85, 0.52, \dots, 5\times 10^{-4}, 1\Big]$